Variationsregning er en gren af matematikken, der omhandler metoder til bestemmelse af mindsteværdi eller størsteværdi for funktioner, som er defineret på givne klasser af kurver, flader eller andre geometriske objekter.
variationsregning
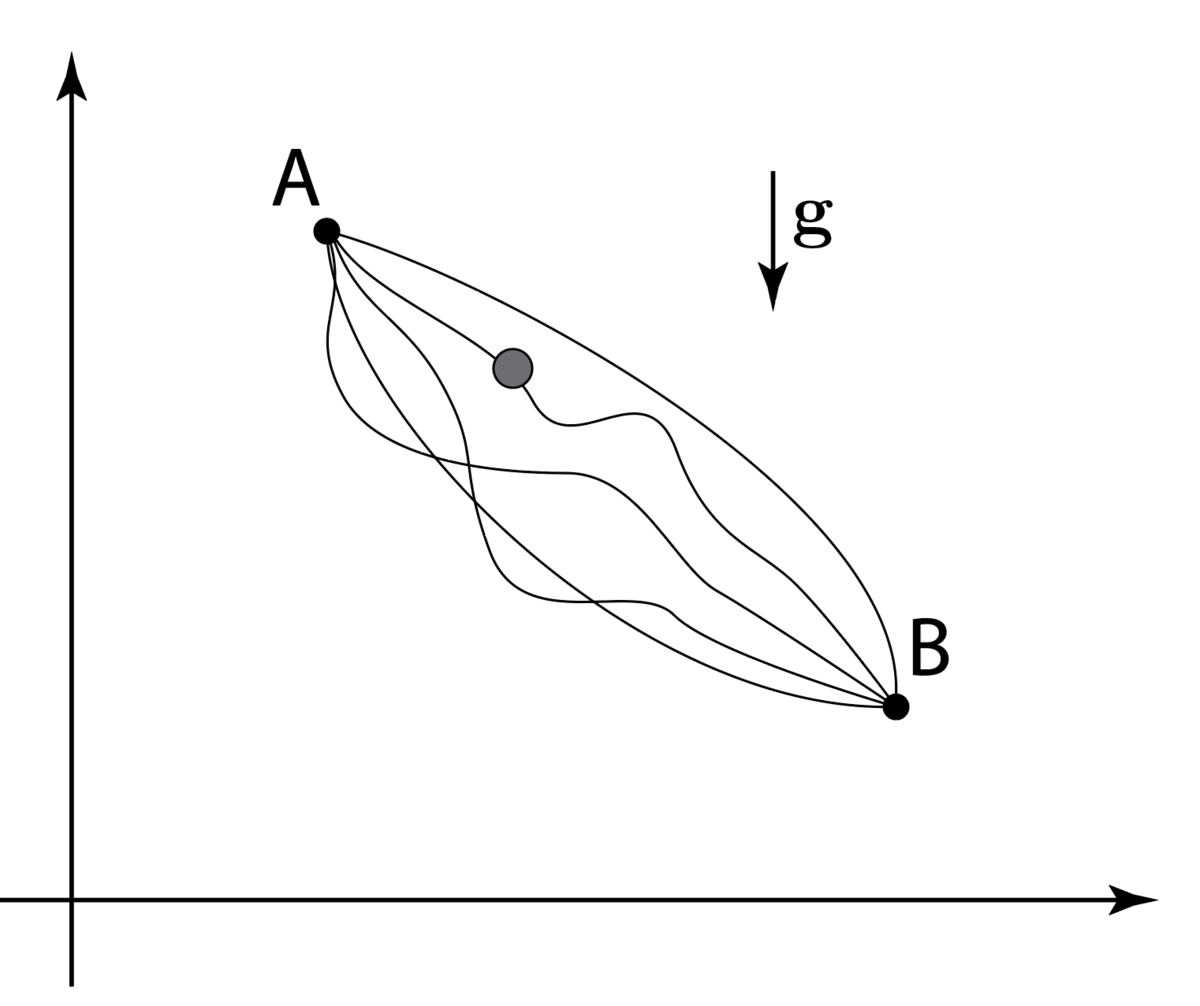
Eksempel: Brachistochron-problemet ('korttidskurven')
Et typisk eksempel er det brachistochrone problem, der blev formuleret og løst i slutningen af 1600-talllet: At finde den kurve, ad hvilken en massepartikel under indvirkning af tyngdekraften hurtigst glider (gnidningsfrit) fra et givet punkt A til et givet (lavere) punkt B. Problemet kan formuleres som at skulle minimere en funktion, der, via et integral langs den ukendte kurve med endepunkter A og B giver den samlede tid partiklen bruger på at glide langs kurven fra A til B.
Sådanne problemer blev studeret generelt af Leonhard Euler og Joseph Louis Lagrange, der fandt et system af differentialligninger, Euler-Lagrange ligningerne, som kurven skal være (en del af) en løsning til, hvis den skal give et maksimum eller et minimum.
Anvendelser i fysik
I fysikken spiller sådanne variationsprincipper en stor rolle, fx i mindste virknings princip og i William Rowan Hamiltons påvisning af, at den klassiske mekaniks ligninger kan formuleres som variationsproblemer vha. passende virknings-integraler. Albert Einsteins almene relativitetsteori kan formuleres og studeres effektivt med variationsregningens begreber og metoder.
Anvendelser i geometri
Variationsregning behandler også problemer, som involverer kurverne eller fladerne selv, fx Plateaus problem, dvs. at finde en minimalflade med en given randkurve. Relateret hertil er de isoperimetriske problemer, hvor man fx skal finde den kurve med en given længde, som i planen omslutter det største areal.
Generalisering
En vigtig generalisering af variationsregningen, udviklet i 1900-tallet, er den såkaldte Morse-teori, der blev grundlagt af Harold Marston Morse i 1920'erne og videreudviklet af bl.a. Stephen Smale. Teorien omhandler især globale aspekter af variationsregningen og har ført til nye resultater i global analyse og topologi.




Kommentarer
Kommentarer til artiklen bliver synlige for alle. Undlad at skrive følsomme oplysninger, for eksempel sundhedsoplysninger. Fagansvarlig eller redaktør svarer, når de kan.
Du skal være logget ind for at kommentere.