Eksponentialfunktion betegner en matematisk funktion af formen \(a^x\), hvor den uafhængige variabel \(x\) optræder som eksponent, og \(a\) er en positiv konstant kaldet grundtallet. Eksponentialfunktionen er defineret ved
\[a^n = \begin{cases} a \cdot a \cdot \cdot \cdot a \ (n\text{ faktorer}), &n=1,2,... \\ 1, &n=0 \\ \frac{1}{a^{n}}, &n=-1,-2,... \end{cases}\]
Eksponentialfunktionen kan defineres for et vilkårligt reelt tal \(x\) på en sådan måde, at den er en kontinuert funktion.
Der gælder de vigtige regneregler
- \(a^{x+y}=a^x \cdot a^y \text{ og}\)
- \({(a^x)}^y = a^{x \cdot y}\),
hvoraf følger, at
- \(a^{-x} = {(\frac{1}{a})}^x = \frac{1}{a^x}\text{ og}\)
- \(a^{\frac{1}{n}}=\sqrt[n]{a}\), for \(n = 2,3,...\) .
Den naturlige eksponentialfunktion \(\exp\) fremkommer, når grundtallet \(a\) er lig med tallet \(e\). Der gælder rækkefremstillingen
\[\exp{(x)}=e^x=1+\frac{x}{1}+\frac{x^2}{1 \cdot 2}+\dots\]
Den omvendte funktion til \(e^x\) er den naturlige logaritme \(\ln{(x)} = \log_e{(x)}\) . Ved hjælp af denne kan alle eksponentialfunktioner udtrykkes ved den naturlige eksponentialfunktion, idet der gælder
\[a^x=e^{x\cdot\ln{(a)}}\]
for \(a>0\) og vilkårligt \(x\).
Funktionen \(f{(x)}=\exp{(kx)}\) er løsning til differentialligningen \(y'=ky\) med begyndelsesbetingelse \(y(0)=1\). Dermed beskriver \(f\) en eksponentiel vækst, hvor væksthastigheden er proportional med den øjeblikkelige størrelse. En eksponentiel vækst \(f\), hvor den øjeblikkelige størrelse fordobles over et fast tidsrum \(T\) (fordoblingstiden), er fastlagt ved \(k=\frac{\ln{(2)}}{T}\).
Ved ovenfor viste rækkeudvikling kan eksponentialfunktionen defineres for komplekst \(x\), hvorved den bliver en holomorf funktion, se Eulers formel.




Kommentarer (4)
skrev Benjamin Schnedler
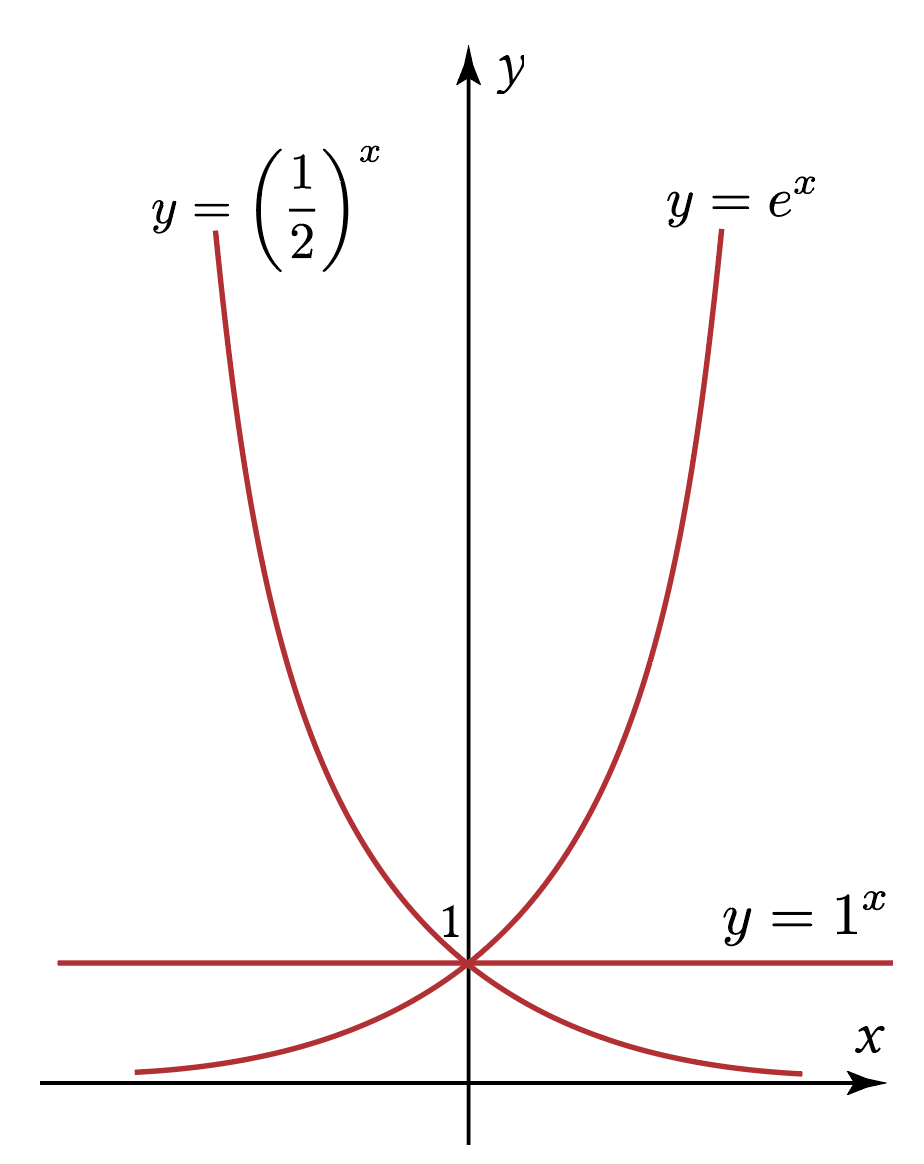
I faktaboksen bør i nok overveje at ændre "a = e, 1, 12." til det som grafen viser altså: "a = e, 1, ½.".
svarede Marie Bilde
Kære Benjamin Schnedler.
Tak for din observation. Jeg har rettet i billedteksten såvel som de øvrige formler, som også var formateret uheldigt.
Venlig hilsen
Marie Bilde, redaktør,
skrev Kristoffer Almdal
Der et par trykfejl i artiklen:
Definition af a^n er forkert for n negativ. Der skal stå 1/a^n ikke 1/a^-n.
Rækkeudviklingen af e^x skal være
1+x/1+x^2/1*2+...
svarede Poul G. Hjorth
Tak Kristoffer. De to trykfejl er ændret nu. Mvh Poul Hjorth
Kommentarer til artiklen bliver synlige for alle. Undlad at skrive følsomme oplysninger, for eksempel sundhedsoplysninger. Fagansvarlig eller redaktør svarer, når de kan.
Du skal være logget ind for at kommentere.