Napiers formler er navnet på fire relationer mellem vinklerne og siderne i en sfærisk trekant.
Faktaboks
- Etymologi
-
efter John Napier
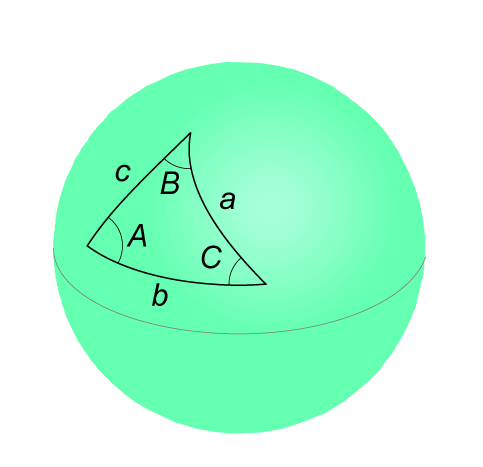
Herunder ses de fire relationer. \(A\), \(B\) og \(C\) er trekantens vinkler, og \(a\), \(b\) og \(c\) er dens sider.
\[\frac{\sin\frac{1}{2}(A-B)}{\sin\frac{1}{2}(A+B)}=\frac{\tan\frac{1}{2}(a-b)}{\tan\frac{1}{2}c}\]
\[\frac{\cos\frac{1}{2}(A-B)}{\cos\frac{1}{2}(A+B)}=\frac{\tan\frac{1}{2}(a+b)}{\tan\frac{1}{2}c}\]
\[\frac{\sin\frac{1}{2}(a-b)}{\sin\frac{1}{2}(a+b)}=\frac{\tan\frac{1}{2}(A-B)}{\cot\frac{1}{2}C}\]
\[\frac{\cos\frac{1}{2}(a-b)}{\cos\frac{1}{2}(a+b)}=\frac{\tan\frac{1}{2}(A+B)}{\cot\frac{1}{2}C}\]




Kommentarer
Kommentarer til artiklen bliver synlige for alle. Undlad at skrive følsomme oplysninger, for eksempel sundhedsoplysninger. Fagansvarlig eller redaktør svarer, når de kan.
Du skal være logget ind for at kommentere.