Arcsin-loven udtrykker i spilteori (for et x mellem 0 og 1) en tilnærmet sandsynlighed for, at en spiller i en række "fair" spil har ført højst \(x\cdot 100%\) af tiden. Den tilnærmede værdi er givet ved arcsin-fordelingens værdi i x, som er lig med tilhørende tæthedsfunktion . Tæthedsfunktionen antager sin mindsteværdi for \(x=1/2\) og sine største værdier for \(x \to 0 \) og \(x \to 1\), hvilket bemærkelsesværdigt betyder, at det er langt mere sandsynligt, at spilleren har ført (eller været bagud) den altovervejende del af tiden, end at have ført ca. halvdelen af tiden. Den præcise formulering af arcsin-loven er knyttet til en random walk med en kontinuert symmetrisk fordelingsfunktion. Beviset for arcsin-loven har givet anledning til en række kombinatoriske metoder, som har haft stor betydning for mange dele af sandsynlighedsteorien. Desuden er arcsin-loven udvidet til at gælde for en række af vigtige størrelser i sandsynligheds- og køteorien samt i fysikken.
arcsin-loven

Arcsin-loven. Tæthedsfunktionen for arcsin-fordelingen; hvert af de fem områder repræsenterer sandsynligheden 0,2. Sandsynligheden for, at en spiller i en række fair spil har ført p% af tiden, vil være bestemt af arcsin-loven. Det ses, at sandsynligheden for at have ført mellem 35% og 65% af tiden kun er 0,2, hvilket er det samme som at have ført mindst 90% af tiden.
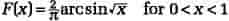
Ukendt.
Licens:
Brukerspesifisert
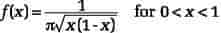
Ukendt.
Licens:
Brukerspesifisert



Kommentarer
Kommentarer til artiklen bliver synlige for alle. Undlad at skrive følsomme oplysninger, for eksempel sundhedsoplysninger. Fagansvarlig eller redaktør svarer, når de kan.
Du skal være logget ind for at kommentere.