Tal, matematisk begreb, som ikke blot omfatter de naturlige tal 1,2,3, ... , men også de successive udvidelser til alle hele tal ... ,−3,−2,−1,0,1,2,3, ... , videre til de rationale tal, dvs. tal, der kan skrives som brøk, fx 8/6 = 4/3, -8/6 = −4/3 og 2/1 = 2, og endelig til de reelle og de komplekse tal.
Ved hver udvidelse udstrækkes regneoperationerne addition '+' og multiplikation '∙' såvel som ordningen '≤' til det nye område på en sådan måde, at gængse regneregler bevares, fx den distributive lov a(b+c) = ab+ac og reglen, at a+c ≤ b+c når a ≤ b. Man må dog give afkald på ordning af de komplekse tal.
Ved udvidelsen fra naturlige til hele tal opnås, at subtraktion altid er mulig, fx er 2−5 = −3, idet −3+5 = 2. Ved den videre udvidelse til rationale tal opnås, at division altid er mulig, bortset fra division med 0, fx er 1/2 :4/3 = 3/8, idet 3/8∙4/3 = = 1/2. Udvidelsen til reelle tal giver et talområde, der tillader grænseovergange (se grænseværdi) og dermed kan bære differential- og integralregning. Hver gang er udvidelsen den mindst mulige.
Illustreres de hele tal på en orienteret ret linje ved punkter med fast afstand, får også hvert rationalt tal sit tilsvarende punkt. Fx fås punktet svarende til 7/3 = 21/3 ved hjælp af en tredeling af stykket fra 2 til 3. Men alle punkter på tallinjen kommer først med ved udvidelsen til reelle tal.
Et reelt tal, der ikke er rationalt, kaldes irrationalt. Et eksempel er , som dog er algebraisk, dvs. rod i en algebraisk ligning med rationale koefficienter, nemlig x2−2 = 0. Tal, der ikke er algebraiske, kaldes transcendente. Eksempler er e og π (pi).
Med tilføjelsen af de irrationale tal er alle "huller" på tallinjen fyldt. Ved den videre udvidelse går man så uden for tallinjen: De komplekse tal svarer til punkterne i en plan, den komplekse plan. De nytilkomne tal kaldes imaginære. Ved udvidelsen opnås, at roduddragning altid er mulig. Fx har ligningen x2 = −1 to rødder, betegnet i og −i, som så begge er værdier af. Der gælder endda, at enhver algebraisk ligning har rødder (algebraens fundamentalsætning).
Udvidelse af de komplekse tal med bevarelse af alle gængse regneregler er ikke mulig. Der findes dog en udvidelse, hvor der blot er givet afkald på den kommutative lov ab = ba ; se kvaternioner.
Mængderne af naturlige, hele, rationale, reelle og komplekse tal betegnes hhv. N, Z, Q, R og C, efter N. Bourbaki. Udvidelse af de naturlige tal i en ganske anden retning tager udgangspunkt i deres anvendelse til angivelse af antal (kardinaltal) eller plads i en rækkefølge (ordinaltal). Den naturlige talrække fortsættes i første tilfælde med transfinite kardinaltal til angivelse af mægtighed af uendelige mængder, i det andet med transfinite ordinaltal til nummerering af elementerne i velordnede mængder, hvor de naturlige tal ikke slår til. Se også mængdelære.
Mængderne N, Z og Q såvel som mængden af algebraiske tal har alle det mindste transfinite kardinaltal ℵ0, mens R og C såvel som mængderne af irrationale, hhv. transcendente tal alle har samme, større kardinaltal ℵ.
Se også p-adisk tal.


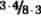

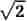
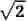
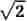

Kommentarer
Kommentarer til artiklen bliver synlige for alle. Undlad at skrive følsomme oplysninger, for eksempel sundhedsoplysninger. Fagansvarlig eller redaktør svarer, når de kan.
Du skal være logget ind for at kommentere.